[Machine Learning]: #3 Parameter Learning

[Machine Learning]: Parameter Learning

The problem is how to solve the math model I post in Bolg [Machine Learning] Model and Cost Function.
-------------------------------
Question and Math Model:

         Hypothesis:                              \({H_\theta }(x) = {\theta _0} + {\theta _1}x\)

         Parameters:                              \({\theta _0}, {\theta _1}\)

         Cost Function:                         \(J({\theta _0},{\theta _1}) = {1 \over {2m}}\sum\nolimits_{i = 1}^m {{{(\hat y_i^{} - {y_i})}^2}}  = {1 \over {2m}}\sum\nolimits_{i = 1}^m {{{({H_\theta }({x_i}) - {y_i})}^2}} \)

         Goal: minimize:                        \(J({\theta _0},{\theta _1})\)
-------------------------------

In this Bolg, we are going to give a general method to solve this question.

1. Gradient Descent

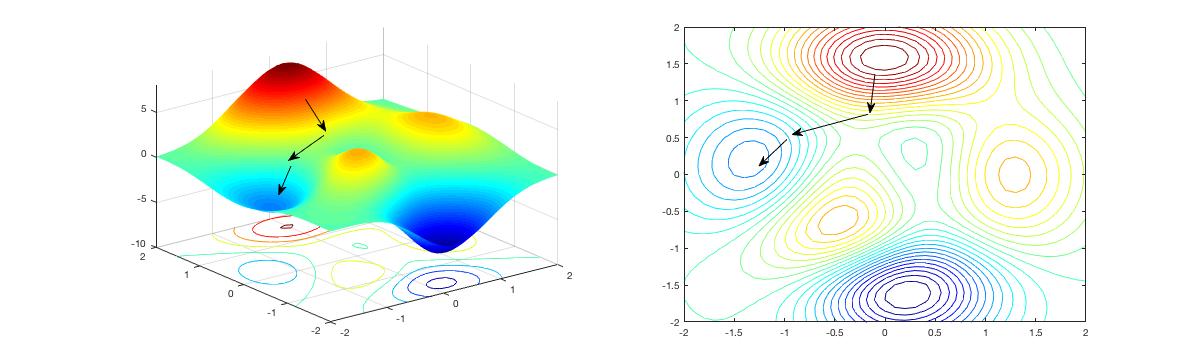
The \(z\) axis is the value of the cost function. and  \({\theta _0}\) and  \({\theta _1}\)  is the \(x\) axis and \(y\) axis. Our goal is to find the minimum the cost function.

The way we do this is by taking the derivative (the tangential line to a function) of our cost function. The slope of the tangent is the derivative at that point and it will give us a direction to move towards. We make steps down the cost function in the direction with the steepest descent. The size of each step is determined by the parameter \({\alpha }\), which is called the learning rate.

For example, the distance between each start in the graph above represents a step determined by our parameter \({\alpha }\),  A smaller \({\alpha }\) would result in a smaller step and a larger \({\alpha }\) results in a larger step. The direction in which the step is taken is determined by the partial derivative of J(θ0,θ1). 

Please note: Depending on where one starts on the graph, one could end up at different points. which means that one start point may help us to get to the global min but another would not and reach to the local min.


2. How to reach to the min?

Here is the gradient descent algo:

Repeat the follows function until it convergence:

$${\theta _j} = {\theta _j} - \alpha {\delta  \over {\delta {\theta _j}}}J({\theta _0},{\theta _1})$$

Important!!!!

For each iteration \(j\), we have to update \({\theta _j}\) simultaneously. Which means that we have to do as following:

$$tem{p_0} = {\theta _0} - \alpha {\delta  \over {\delta {\theta _0}}}J({\theta _0},{\theta _1})$$

$$tem{p_1} = {\theta _1} - \alpha {\delta  \over {\delta {\theta _1}}}J({\theta _0},{\theta _1})$$

$${\theta _0} = tem{p_0}$$

$${\theta _1} = tem{p_1}$$

3. More about the Learning Rate \({\alpha }\) 

• if the  \({\alpha }\)  is too small, we have to use more time to get to the opt. Because the learning rate is too small. Every time we update \({\theta _j}\), it changes a little.

• If the  \({\alpha }\)  is too big, then we study too much and can't reach to the opt.

• if we have already at the local opt, the \({\theta _j}\) not change.

4. Gradient Descent For Linear Regression

From the equation above, we can modify our equations to:

repeat until convergence: {θ0:=θ1:=}θ0−α1m∑i=1m(hθ(xi)−yi)θ1−α1m∑i=1m((hθ(xi)−yi)xi)Our job i

Our job is to repeat the above function and stop when it converged. Please note that we have to use the entire training set on every step, and this is called batch gradient descent.

5. Summary of our First Machine Learning Algo:

Our goal is to min the Cost Function, and the realted functions are given as follows:

         Hypothesis:                              \({H_\theta }(x) = {\theta _0} + {\theta _1}x\)

         Parameters:                              \({\theta _0}, {\theta _1}\)

         Cost Function:                         \(J({\theta _0},{\theta _1}) = {1 \over {2m}}\sum\nolimits_{i = 1}^m {{{(\hat y_i^{} - {y_i})}^2}}  = {1 \over {2m}}\sum\nolimits_{i = 1}^m {{{({H_\theta }({x_i}) - {y_i})}^2}} \)


         Goal: minimize:                        \(J({\theta _0},{\theta _1})\)

--> In order to min the Cost Function, the first step comes to my mind is using Gradient Descent. So we use partial derivate to get the following:
$$J({\theta _0},{\theta _1}) = {1 \over {2m}}\sum\limits_{i = 1}^m {{{(H(x) - {y_i})}^2}} $$
$$\left\{ \matrix{
  {\theta _0} = {\theta _0} - \alpha {\delta  \over {\delta {\theta _0}}}J({\theta _0},{\theta _1}) \hfill \cr
  {\theta _1} = {\theta _1} - \alpha {\delta  \over {\delta {\theta _1}}}J({\theta _0},{\theta _1}) \hfill \cr}  \right.$$
repeat until convergence: {θ0:=

}

--> Then we put our Hypothesis Function into the function above and get the follows:

$$\left\{ \matrix{
  {\theta _0} = {\theta _0} - \alpha {1 \over m}\sum\limits_{i = 1}^m {({\theta _0} + {\theta _1}{x_i} - {y_i})}  \hfill \cr
  {\theta _1} = {\theta _1} - \alpha {1 \over m}\sum\limits_{i = 1}^m {(({\theta _0} + {\theta _1}{x_i} - {y_i}){x_i})}  \hfill \cr}  \right.$$

--> We use our training data set to train the function above and repeat until it converges.