Question:
Given a binary search tree, write a function
kthSmallest to find the kth smallest element in it.
************************************************************************************************************************************
Write Infront
To read to a tutorial, please to read the tutorial of in-order traversal of BST, please check:
LeetCode Solution 94: Binary Tree Inorder Traversal
We are going to solve this question using the following 4 methods:
->Binary Search
->Recursive
->Iterative
->Morris
LeetCode Solution 94: Binary Tree Inorder Traversal
We are going to solve this question using the following 4 methods:
->Binary Search
->Recursive
->Iterative
->Morris
Approach #1 Binary Search [Accepted]
Detail Explanation
The first method to solve this problem is using Binary Search.
The idea is very easy and extremely to think.
We use BST's property that the left child of the root is smaller than the root
while the right child of the root is always bigger.
We consider that the root is the pivot,
and find the number of the nodes in the left subtree
and the number of the nodes in the right subtree,
then go into the subtree that the Kth Smallest Value Node belongs to.
The first method to solve this problem is using Binary Search.
The idea is very easy and extremely to think.
We use BST's property that the left child of the root is smaller than the root
while the right child of the root is always bigger.
We consider that the root is the pivot,
and find the number of the nodes in the left subtree
and the number of the nodes in the right subtree,
then go into the subtree that the Kth Smallest Value Node belongs to.
Java
class Solution {
public int kthSmallest(TreeNode root, int k) {
int counter = helper(root.left);
if(k<=counter)
{
return kthSmallest(root.left, k);
}
else if(k > counter+1)
{
return kthSmallest(root.right, k-1-counter);
}
return root.val;
}
public int helper(TreeNode root)
{
if(root == null) return 0;
return 1+helper(root.left)+helper(root.right);
}
}
Complexity Analysis
- Time complexity : $$O(log(k))$$.
- Space complexity : $$O(k)$$
Approach #2 Recursive [Accepted]
Detail Explaination
This is the classical method and straightforward. we can define a helper function to implement recursion.
The JAVA code is as follows:
This is the classical method and straightforward. we can define a helper function to implement recursion.
The JAVA code is as follows:
Java
class Solution {
private static int counter;
private static int res;
public int kthSmallest(TreeNode root, int k) {
counter = k;
helper(root, k);
return res;
}
public void helper(TreeNode root, int k) {
if (root == null)
return;
if (root.left != null) {
helper(root.left, k);
}
counter--;
if(counter == 0)
{
res = root.val;
return;
}
if (root.right != null) {
helper(root.right, k);
}
}
}
Complexity Analysis
- Time complexity : $$O(k)$$.
- Space complexity : $$O(k)$$.
Approach #3 Iterating method using Stack [Accepted]
Detail Explanation
The strategy is very similar to the iterative method in in-order traversal BST,
the only different is we have to use a counter to count the node we are visiting,
if it is the Kth node we poped from the stack, return.
The strategy is very similar to the iterative method in in-order traversal BST,
the only different is we have to use a counter to count the node we are visiting,
if it is the Kth node we poped from the stack, return.
Java
class Solution {
public int kthSmallest(TreeNode root, int k) {
int counter = 0;
Stack<TreeNode> stack = new Stack<>();
TreeNode curr = root;
while(curr!=null||!stack.isEmpty())
{
while(curr!= null)
{
stack.push(curr);
curr = curr.left;
}
curr = stack.pop(); counter ++;
if(counter == k)
{
return curr.val;
}
curr = curr.right;
}
return 0;
}
}
Complexity Analysis
- Time complexity : $$O(k)$$.
- Space complexity : $$O(k)$$.
Approach #4 Morris Traversal [Accepted]
Detail Explanation
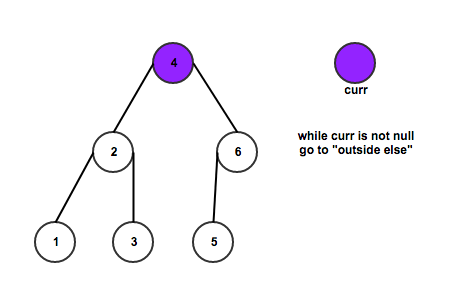
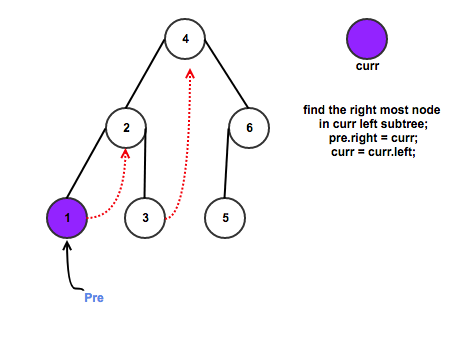
This method we have to use a new data structure Threaded Binary Tree and the strategy is as follows:
This method we have to use a new data structure Threaded Binary Tree and the strategy is as follows:
Step1. Initialize current as root, counter is 0 and result as the min value;
Step2. While current is not NULL
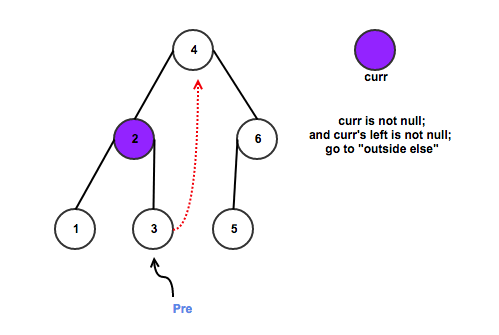
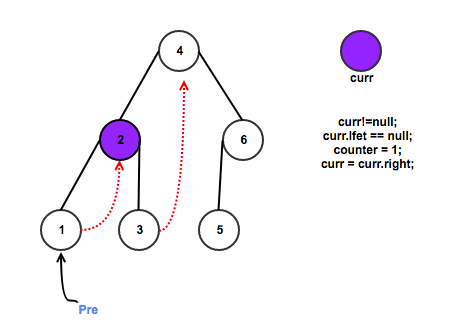
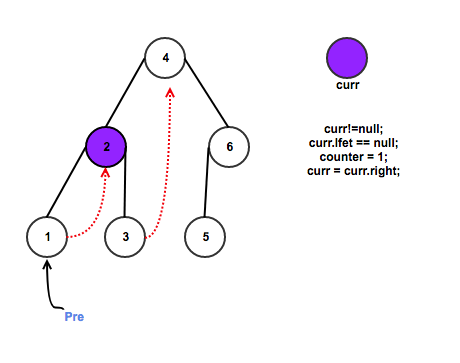
If current does not have left child
a. counter++;
b. check the counter value, if the counter equals k, return.
c. Go to the right, i.e., current = current.right
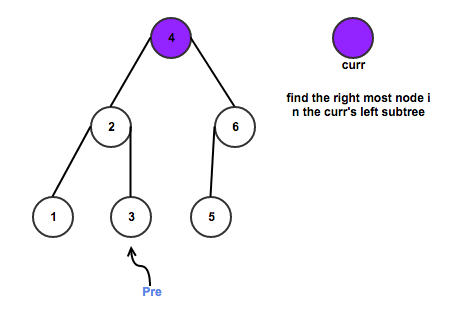
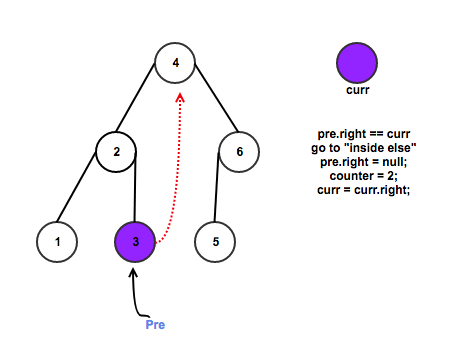
Else
a. Denote pre as the left child of current node;
b. In current left subtree, make current right the right child of the rightmost node
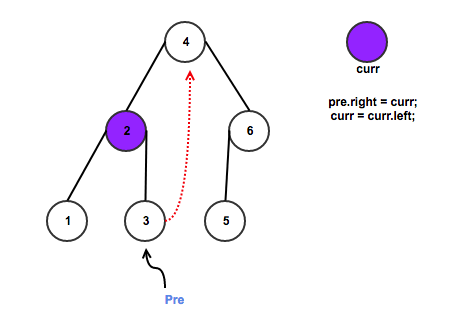
c. If right most node do not have right child, we set its left child as current node, and update current to its left;
d. Else we set right most node right child as null, update and check counter, set current as its right.
For Example: k = 3
Java
class Solution {
public int kthSmallest(TreeNode root, int k) {
int counter = 0;
int res = Integer.MIN_VALUE;
TreeNode curr = root;
while (curr != null) {
if (curr.left == null) {
counter++;
if (counter == k) {
res = curr.val;
}
curr = curr.right;
} else {
TreeNode pre = curr.left;
while (pre.right != null && pre.right != curr) {
pre = pre.right;
}
if (pre.right == null) {
pre.right = curr;
curr = curr.left;
} else {
pre.right = null;
counter++;
if (counter == k)
res = curr.val;
curr = curr.right;
}
}
}
return res;
}
}
Complexity Analysis
- Time complexity : $$O(n)$$. To prove that the time complexity is $$O(n)$$,
the biggest problem lies in finding the time complexity of finding the predecessor nodes of all the nodes in the binary tree.
Intuitively, that complexity is $$O(nlgn)$$, because to find the predecessor node for a single node related to the height of the tree.
But in fact, finding the predecessor nodes for all nodes only needs $$O(n)$$ time. Because n nodes in a Binary-Tree have n-1 edges, the whole processing for each edges up to 2 times, one is to locate a node, and the other is to find the predecessor node.
So the complexity is $$O(n)$$. - Space complexity : $$O(1)$$. We only need pointer curr and pre.

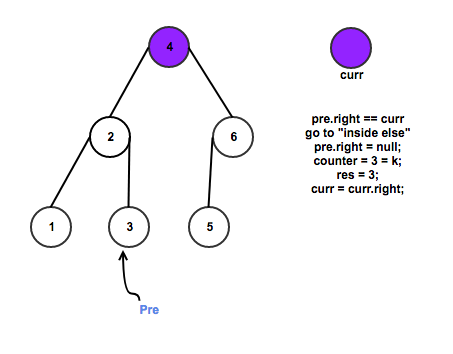
The time complexity of Approach 1 is still O(k), because despite the recursion depth is O(nlogk), the runtime of helper() is not O(1).
ReplyDeleteFirst solution's time complexity is O(n). Please correct it
ReplyDelete