[Machine Learning] #9 Multi-class Classification

[Machine Learning] #9 Multi-class Classification

[Write Infront]:

Binary classification posted in the previous blog [Machine Learning]: #8 Logistic Model. The picture (Allen Turing) is different from the previous one no tense expression, so topic today seems like much easier to understand...😃

*********************************************************************************

*********************************************************************************

[Muti-Classification]

The different is we want to seperate the output in diferent class, that's it! Instead of \(y = \{ 0, 1\}\), we will expand our defination so that  \(y = \{ 0, 1, 2, 3 ..., n\}\).

So, for each \(y\), we have to divide our problem into \(n+1\)binary classification problems. In each one, we predict the probability that 'y' is a member of one of our classes.
$$\eqalign{
  & y \in \{ 0,1,......n\}   \cr
  & H_\theta ^0(x) = P(y = 0|x,\theta )  \cr
  & H_\theta ^1(x) = P(y = 1|x,\theta )  \cr
  & ......  \cr
  & H_\theta ^n(x) = P(y = n|x,\theta )  \cr
  & prediction = \mathop {\max }\limits_i (H_\theta ^i(x)) \cr} $$

We are basically choosing one class and then wrapping all the other into one single second class. We repeatedly, applying binary logistic regression to each case, and then use the hypothesis that returns the highest value of prediction.

*********************************************************************************
[An Example]:

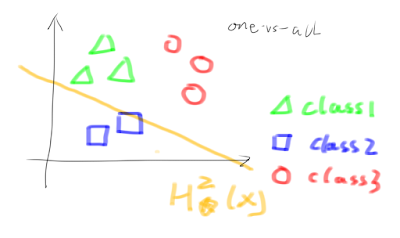
As shown in the picture above, we have 3 classes, first we just want to seperate class1(th green one), so we have to find the logistic regression classifier \(H_\theta ^1(x)\)

$$H_\theta ^1(x) = P(y = 1|x,\theta )$$

Then, we use the same strategy on class2.

$$H_\theta ^2(x) = P(y = 2|x,\theta )$$

$$H_\theta ^3(x) = P(y = 3|x,\theta )$$

To make a prediction on a new \(x\), pick the class that have the \(\mathop {\max }\limits_i (H_\theta ^i(x))\) where \(i={1,2,3}\)