Question: Validate Binary Search Tree
Given a binary tree, determine if it is a valid binary search tree (BST).
Assume a BST is defined as follows:
The left subtree of a node contains only nodes with keys less than the node’s key.
The right subtree of a node contains only nodes with keys greater than the node’s key.
Both the left and right subtrees must also be binary search trees.
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
The right subtree of a node contains only nodes with keys greater than the node’s key.
Both the left and right subtrees must also be binary search trees.
Write Before
The problem is same to the BST Inorder Traversal: LeetCode 94 !!! Why?
Because the inorder traversal get the order from root.left -> root -> root.right,
if the ValidBST is true, the inorder traversal is ascending order.
How to implement inorder traversal in BST?
->Recursive Method
->Iterative Method
->Morris Method
The tutorial following have all the detail of inorder traversal.
BST inorder Traversal
Because the inorder traversal get the order from root.left -> root -> root.right,
if the ValidBST is true, the inorder traversal is ascending order.
->Recursive Method
->Iterative Method
->Morris Method
BST inorder Traversal
Approach #1.1 Recursive [Accepted]
Detail Explanation
The first method to solve this problem is using recursive.
This is the classical method and straightforward. we can define a helper function to implement recursion.
We use the property of the BST, where root.left.value< root.value< root.right.value
The Java code is as follows:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
Complexity Analysis
-
Time complexity:
O(n) . The time complexity is O(n) because the recursive function is T(n)=2∗T(n/2)+1 .
-
Space complexity:
O(n) .
The first method to solve this problem is using recursive.
This is the classical method and straightforward. we can define a helper function to implement recursion.
We use the property of the BST, where root.left.value< root.value< root.right.value
The Java code is as follows:
Time complexity: O(n) . The time complexity is O(n) because the recursive function is T(n)=2∗T(n/2)+1 .
Space complexity: O(n) .
Approach #1.2 Inorder Traversal(Recursive + ArrayList) [Accepted]
Detail Explanation
Using recursive method to traverse BST and put the value into an array,
then check if the array is ordered or not.
Java
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
Complexity Analysis
-
Time complexity:
O(n) . The recursive complexity is O(n) and we have to traverse the array then where time complexity is O(n) .
So the overall time complexity is 2∗O(n) equal to O(n) .
-
Space complexity: The worst case for recursive is
O(n) , and we need O(n) extra space for the array, So the overall time complexity is 2O(n) equal to O(n) .
then check if the array is ordered or not.
Time complexity: O(n) . The recursive complexity is O(n) and we have to traverse the array then where time complexity is O(n) .
So the overall time complexity is2∗O(n) equal to O(n) .
So the overall time complexity is
Space complexity: The worst case for recursive is O(n) , and we need O(n) extra space for the array, So the overall time complexity is 2O(n) equal to O(n) .
Approach #1.3 Inorder Traversal(Recursive Without ArrayList) [Accepted]
Detail Explanation
We can compare the value in the helper function.
This is almost same method strategy above,
the only change is instead of adding the value into the result list,
we have to check if the current value is larger than the previous one.
So, we need a poniter “preNode” and a flag,
where flag change its value only if this is not valid BST.
Java
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
Complexity Analysis
- Time complexity:
O(n) . The recursive complexity is O(n) but the worst case to find the tree is not the Valid BST still need O(n) .
So the overall time complexity is 2∗O(n) equal to O(n) .
- Space complexity:
O(n) .
We can compare the value in the helper function.
This is almost same method strategy above,
the only change is instead of adding the value into the result list,
we have to check if the current value is larger than the previous one.
So, we need a poniter “preNode” and a flag,
where flag change its value only if this is not valid BST.
So the overall time complexity is
Approach #2 Inorder Traversal(Iterative Method) [Accepted]
Detail Explanation
We need a stack to implement this method. Similiar to the inorder traversal, the only difference is we have curr pointer and pre pointer,
every time we pop from stack, we have to check the value of curr and pre.
Java
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
We need a stack to implement this method. Similiar to the inorder traversal, the only difference is we have curr pointer and pre pointer,
every time we pop from stack, we have to check the value of curr and pre.
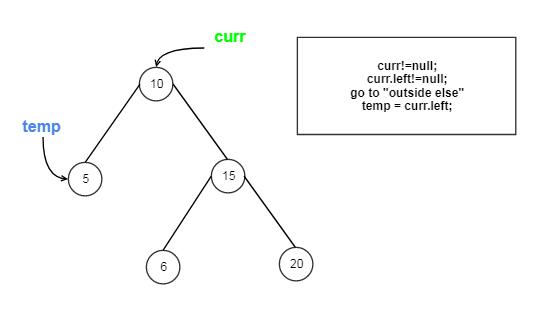
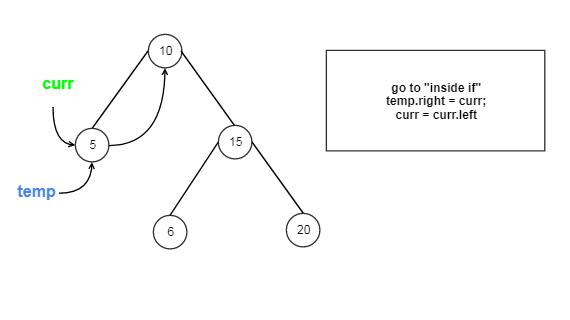
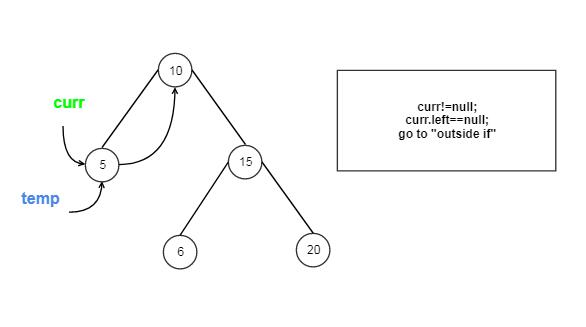
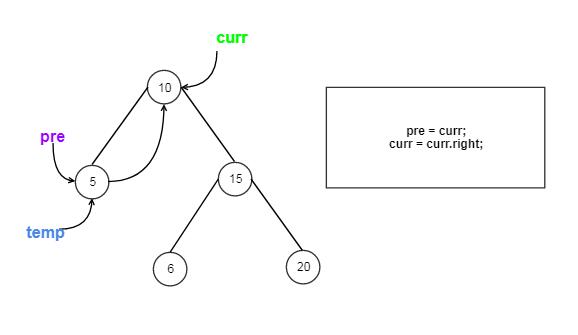
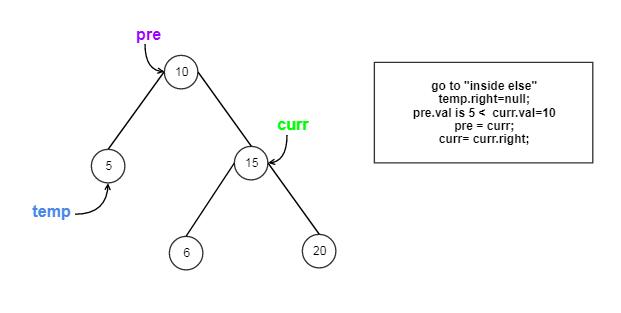
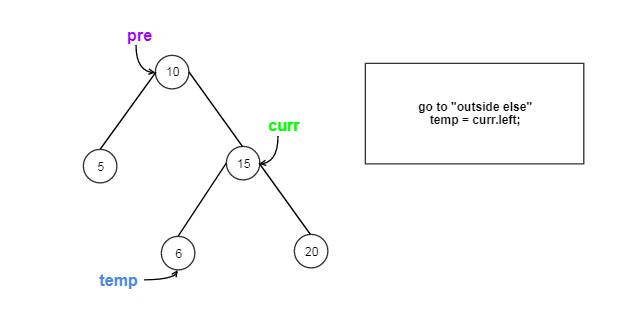
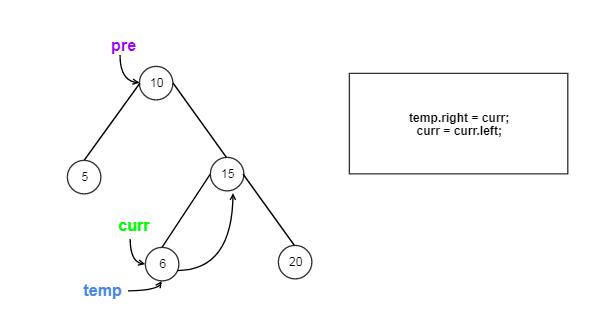
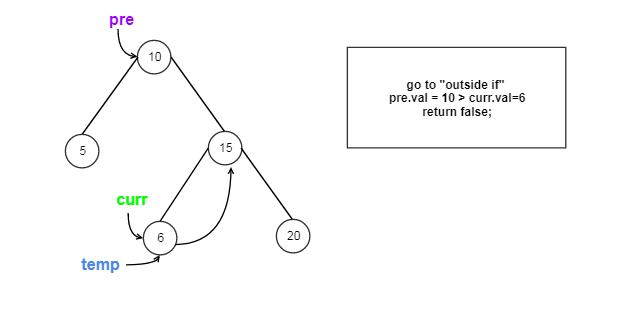
Approach #3 Inorder Traversal(Morris Method) [Accepted]
Detail Explanation
The strategy is similar to the Morris Method in Inorder BST Traversal problem, but we need 3 extra pointers.
The Java code is as follows:
Java
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
How it works?
Let us Go through the coding step by step:

 Complexity Analysis
Complexity Analysis
- Time complexity:
O(n) .
- Space complexity:
O(1) . The space complexity of Morris Traversal is O(1) because it just needs 3 “assisting” pointers. (TreeNode curr, TreeNode temp and TreeNode pre)
The strategy is similar to the Morris Method in Inorder BST Traversal problem, but we need 3 extra pointers.
The Java code is as follows:
Let us Go through the coding step by step:










Comments
Post a Comment